DEMOSTRACIÓN GEOMÉTRICA DEL CUADRADO DE UN BINOMIO
Productos notables
Productos notables es el nombre que reciben multiplicaciones con expresiones algebraicas que cumplen ciertas reglas fijas, cuyo resultado se puede escribir mediante simple inspección, sin verificar la multiplicación.
Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados, y recíprocamente.
Cuadrado de un binomio
Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Así:
| Demostración |
La expresión siguiente: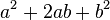 
se conoce como trinomio cuadrado perfecto.
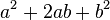se conoce como trinomio cuadrado perfecto.
Cuando el segundo término es negativo, la igualdad que se obtiene es:
| Demostración |
Ejemplo:
Simplificando:
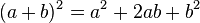
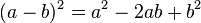
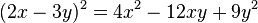
No hay comentarios:
Publicar un comentario