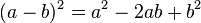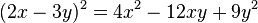SISTEMA SEXAGESIMAL

El Sistema Sexagesimal es un sistema de numeración en el que cada unidad se divide en 60 unidades de orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad a la medida del tiempo y a la de la amplitud de los ángulos.

                       1 h  60 min  60 s

1º  60'  60''

RELACIÓN ENTRE RADIANES Y GRADOS SEXAGESIMALES

Se parte de la base de que una circunferencia completa tiene  radianes, y que una circunferencia tiene 360° sexagesimales, luego tenemos:

Haciendo una regla de tres simple se llega a que el factor de conversión de grados sexagesimales a radianes es:

Luego tenemos que, para un ángulo x dado en grados, su equivalente X en radianes es:

y viceversa (si tenemos que, para un ángulo X dado en radianes, su equivalente x en grados es):

Slideshare




Mega

Dropbox

Actividad Integradora de Power Point

Powtoon

Recursos Tecnológicos from FatymaLiss

Vialogues

Prezi

Piktochart

Infografía

DEMOSTRACIÓN GEOMÉTRICA DEL CUADRADO DE UN BINOMIO

Productos notables

Productos notables es el nombre que reciben multiplicaciones con expresiones algebraicas que cumplen ciertas reglas fijas, cuyo resultado se puede escribir mediante simple inspección, sin verificar la multiplicación.

Cada producto notable corresponde a una fórmula de factorización. Por ejemplo, la factorización de una diferencia de cuadrados perfectos es un producto de dos binomios conjugados, y recíprocamente.

Cuadrado de un binomio

Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Así:

Demostración

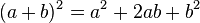
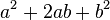La expresión siguiente:  se conoce como trinomio cuadrado perfecto.

Cuando el segundo término es negativo, la igualdad que se obtiene es:

Demostración

Ejemplo:

Simplificando:

VER MÁS

Cuadrado de un binomio from Lgarciaazorero